- DIOPHANTIENNES (ÉQUATIONS)
- DIOPHANTIENNES (ÉQUATIONS)Diophante d’Alexandrie, vers les années 250 de notre ère, fut le premier à rechercher systématiquement les solutions en nombres entiers, ou rationnels, d’une équation ou d’un système d’équations polynomiales à coefficients entiers. Bien que ce ne soit qu’avec Fermat (1601-1665) que les méthodes utilisées pour résoudre ces équations prirent un aspect vraiment arithmétique, c’est-à-dire faisant pleinement intervenir la factorisation des nombres entiers, une longue tradition appelle équation diophantienne la donnée d’un système d’équations polynomiales à coefficients entiers:
 Selon que l’on veut résoudre en nombre entiers ou rationnels, les méthodes et les résultats diffèrent souvent sensiblement.Des méthodes générales existent pour résoudre un système d’équations du premier degré, ou encore une équation du second degré. On dispose encore de méthodes pour étudier une équation du troisième degré, mais déjà, là, les problèmes ouverts abondent. Quant aux équations de degré supérieur, il est significatif que beaucoup d’ouvrages consacrés aux équations diophantiennes n’apparaissent que comme une accumulation de résultats disparates.De fait, il a maintenant été établi (J. Robinson, Yu. V. Matijasevic, 1970) que le dixième problème de Hilbert (cf. problèmes de HILBERT) a une réponse négative: il n’existe pas d’algorithme universel permettant de décider si une équation diophantienne a une solution en nombre entiers.On ne peut donc espérer obtenir des méthodes générales que pour des types particuliers de systèmes d’équations. Comment classifier ces «types»? La façon la plus évidente est d’utiliser le degré des équations définissant le système. Cette classification est souvent trop grossière, mais peut être affinée grâce à la géométrie algébrique. Cette dernière permet d’obtenir des résultats généraux – parfois difficiles à traduire en termes d’équations concrètes. La géométrie algébrique nous donne aussi la mesure de notre ignorance: ainsi aucun changement de variables ne permet de ramener une équation du type:
Selon que l’on veut résoudre en nombre entiers ou rationnels, les méthodes et les résultats diffèrent souvent sensiblement.Des méthodes générales existent pour résoudre un système d’équations du premier degré, ou encore une équation du second degré. On dispose encore de méthodes pour étudier une équation du troisième degré, mais déjà, là, les problèmes ouverts abondent. Quant aux équations de degré supérieur, il est significatif que beaucoup d’ouvrages consacrés aux équations diophantiennes n’apparaissent que comme une accumulation de résultats disparates.De fait, il a maintenant été établi (J. Robinson, Yu. V. Matijasevic, 1970) que le dixième problème de Hilbert (cf. problèmes de HILBERT) a une réponse négative: il n’existe pas d’algorithme universel permettant de décider si une équation diophantienne a une solution en nombre entiers.On ne peut donc espérer obtenir des méthodes générales que pour des types particuliers de systèmes d’équations. Comment classifier ces «types»? La façon la plus évidente est d’utiliser le degré des équations définissant le système. Cette classification est souvent trop grossière, mais peut être affinée grâce à la géométrie algébrique. Cette dernière permet d’obtenir des résultats généraux – parfois difficiles à traduire en termes d’équations concrètes. La géométrie algébrique nous donne aussi la mesure de notre ignorance: ainsi aucun changement de variables ne permet de ramener une équation du type: (a , b , c , d entiers non nuls), à résoudre en (x , y , z ) nombres rationnels, à un type d’équations que l’on sait actuellement traiter.Par extension, on appelle aussi équations diophantiennes des équations dans lesquelles les exposants figurent parmi les inconnues; la plus fameuse équation de ce type est:
(a , b , c , d entiers non nuls), à résoudre en (x , y , z ) nombres rationnels, à un type d’équations que l’on sait actuellement traiter.Par extension, on appelle aussi équations diophantiennes des équations dans lesquelles les exposants figurent parmi les inconnues; la plus fameuse équation de ce type est: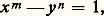 à résoudre en entiers (x , y , m , n ) au moins égaux à 1, qui n’admettrait (E. Catalan, 1814-1894) que la solution:
à résoudre en entiers (x , y , m , n ) au moins égaux à 1, qui n’admettrait (E. Catalan, 1814-1894) que la solution: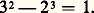 De grands progrès ont été réalisés dans cette direction.Dans cet article, l’ensemble des entiers naturels est désigné par N, l’anneau des entiers relatifs par Z, le corps des nombres rationnels par Q.1. Le premier et le second degréLe premier degréL’équation:
De grands progrès ont été réalisés dans cette direction.Dans cet article, l’ensemble des entiers naturels est désigné par N, l’anneau des entiers relatifs par Z, le corps des nombres rationnels par Q.1. Le premier et le second degréLe premier degréL’équation: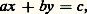 Si c n’est pas divisible par le plus grand commun diviseur de a et b , il n’y a pas de solution entière; on peut donc supposer a et b premiers entre eux et utiliser la résolution de au + bv = 1 (Bezout), d’où x = u 0c + kb , y + v 0c 漣 ka , avec u 0 et v 0 solution particulière de l’équation de Bezout et k entier relatif quelconque.La solution (u 0, v 0) peut se trouver par essais successifs, si a et b ne sont pas trop grands; sinon, on développe a /b en fraction continuée (cf. approximations DIOPHANTIENNES) et, si a /b = p n /q n est la n -ième réduite, on prend la (n 漣 1)-ième qui, au signe près, donne u 0 = q n-1 et v 0 = 漣 p n-1 . Par exemple, si 355 x + 113 y = 1, on a 355/113 = [3, 7, 16], d’où p n-1 /q n-1 = 22/7 et u 0 = 漣 7, v 0 = 22. Cela correspond aussi, si l’on veut, à l’application de l’algorithme d’Euclide au couple (a , b ).L’équation:
Si c n’est pas divisible par le plus grand commun diviseur de a et b , il n’y a pas de solution entière; on peut donc supposer a et b premiers entre eux et utiliser la résolution de au + bv = 1 (Bezout), d’où x = u 0c + kb , y + v 0c 漣 ka , avec u 0 et v 0 solution particulière de l’équation de Bezout et k entier relatif quelconque.La solution (u 0, v 0) peut se trouver par essais successifs, si a et b ne sont pas trop grands; sinon, on développe a /b en fraction continuée (cf. approximations DIOPHANTIENNES) et, si a /b = p n /q n est la n -ième réduite, on prend la (n 漣 1)-ième qui, au signe près, donne u 0 = q n-1 et v 0 = 漣 p n-1 . Par exemple, si 355 x + 113 y = 1, on a 355/113 = [3, 7, 16], d’où p n-1 /q n-1 = 22/7 et u 0 = 漣 7, v 0 = 22. Cela correspond aussi, si l’on veut, à l’application de l’algorithme d’Euclide au couple (a , b ).L’équation: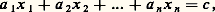 que nous écrirons A . X = c avec:
que nous écrirons A . X = c avec: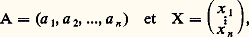 se résout en supposant, les a i premiers entre eux dans leur ensemble, par les points d’un réseau à (n 漣 1) dimensions (cf. approximations DIOPHANTIENNES, chap. 1):
se résout en supposant, les a i premiers entre eux dans leur ensemble, par les points d’un réseau à (n 漣 1) dimensions (cf. approximations DIOPHANTIENNES, chap. 1):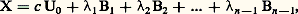 où U0 est solution particulière de l’équation de Bezout A . X = 1 et où B1, B2, ..., Bn-1 engendrent le module des solutions de A . X = 0.Un système non homogène :
où U0 est solution particulière de l’équation de Bezout A . X = 1 et où B1, B2, ..., Bn-1 engendrent le module des solutions de A . X = 0.Un système non homogène :
 avec Vi et C vecteurs colonnes de Zr . Une condition nécessaire et suffisante de résolution est que tous les déterminants d’ordre r extraits de la matrice des coordonnées de (C, V1, V2, ..., Vn ) soient divisibles par le P.G.C.D. des déterminants d’ordre r extraits de la matrice des coordonnées de (V1, V2, ..., Vn ).Signalons que le théorème des restes chinois (x 令 a i mod m i , pour i = 1, 2, ..., r ) correspond à un cas non homogène, avec n = r + 1. Il se ramène, si les m i sont premiers deux à deux, à une seule équation: x 令 a mod m , avec m = m 1 m 2 ... m r .Généralités sur le second degréLa résolution en entiers de:
avec Vi et C vecteurs colonnes de Zr . Une condition nécessaire et suffisante de résolution est que tous les déterminants d’ordre r extraits de la matrice des coordonnées de (C, V1, V2, ..., Vn ) soient divisibles par le P.G.C.D. des déterminants d’ordre r extraits de la matrice des coordonnées de (V1, V2, ..., Vn ).Signalons que le théorème des restes chinois (x 令 a i mod m i , pour i = 1, 2, ..., r ) correspond à un cas non homogène, avec n = r + 1. Il se ramène, si les m i sont premiers deux à deux, à une seule équation: x 令 a mod m , avec m = m 1 m 2 ... m r .Généralités sur le second degréLa résolution en entiers de: équation de conique à coefficients entiers, n’est intéressante que dans les cas parabolique ou hyperbolique. L’étude en a été faite par Euler et Lagrange. Dans le cas elliptique, en effet, il n’y a qu’un nombre fini (éventuellement nul) de solutions, qu’on peut déterminer par essais successifs. C’est ainsi que Gauss a étudié l’équation ax 2 + by 2 = m , avec a et b entiers positifs.Dans le cas parabolique , on pose 2 ax + by = t , d’où 4 adx + 4 aey = 漣 t 2 漣 4 ak et la résolution, lorsqu’elle est possible, conduit à des formules du type:
équation de conique à coefficients entiers, n’est intéressante que dans les cas parabolique ou hyperbolique. L’étude en a été faite par Euler et Lagrange. Dans le cas elliptique, en effet, il n’y a qu’un nombre fini (éventuellement nul) de solutions, qu’on peut déterminer par essais successifs. C’est ainsi que Gauss a étudié l’équation ax 2 + by 2 = m , avec a et b entiers positifs.Dans le cas parabolique , on pose 2 ax + by = t , d’où 4 adx + 4 aey = 漣 t 2 漣 4 ak et la résolution, lorsqu’elle est possible, conduit à des formules du type: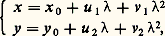 où x 0, y 0, u 1, v 1, u 2, v 2 sont des entiers fixés et où parcourt Z. De telles formules nécessitent, en général, diverses constantes pour donner toutes les solutions.Par exemple: 4 x 2 漣 20 xy + 25 y 2 + 14 x 漣 41 y + 18 = 0 conduit aux quatre systèmes de solutions:
où x 0, y 0, u 1, v 1, u 2, v 2 sont des entiers fixés et où parcourt Z. De telles formules nécessitent, en général, diverses constantes pour donner toutes les solutions.Par exemple: 4 x 2 漣 20 xy + 25 y 2 + 14 x 漣 41 y + 18 = 0 conduit aux quatre systèmes de solutions: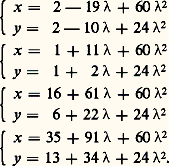 Dans le cas hyperbolique , on se ramène au centre de coordonnées rationnelles 見 = p / , 廓 = q / , et on pose x = (p + X)/ , y = (q + Y)/ , qui conduit à:
Dans le cas hyperbolique , on se ramène au centre de coordonnées rationnelles 見 = p / , 廓 = q / , et on pose x = (p + X)/ , y = (q + Y)/ , qui conduit à: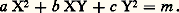
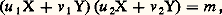 d’où la résolution par un nombre fini de systèmes linéaires:
d’où la résolution par un nombre fini de systèmes linéaires:
 (liées aux unités de Q (face=F0019 連d ), comme on le voit à propos des équations de Pell). On obtient alors les solutions de:
(liées aux unités de Q (face=F0019 連d ), comme on le voit à propos des équations de Pell). On obtient alors les solutions de: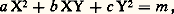 à partir d’un nombre fini d’entre elles. Il peut d’ailleurs n’y avoir aucune solution, comme, par exemple, pour x 2 漣 3 y 2 = 漣 1.
à partir d’un nombre fini d’entre elles. Il peut d’ailleurs n’y avoir aucune solution, comme, par exemple, pour x 2 漣 3 y 2 = 漣 1.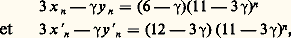 où 塚 = 1 + 連7 est racine de 塚2 漣 2 塚 漣 6 = 0 et où (11 漣 3 塚)n correspond aux solutions de u 2 漣 2 uv 漣 6 v 2 = 1.Équation de PellL’équation de Pell:
où 塚 = 1 + 連7 est racine de 塚2 漣 2 塚 漣 6 = 0 et où (11 漣 3 塚)n correspond aux solutions de u 2 漣 2 uv 漣 6 v 2 = 1.Équation de PellL’équation de Pell: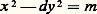 (appelée également équation de Pell-Fermat), où l’on suppose d sans facteur carré, joue un rôle particulier dans les équations du second degré; elle est, en effet, fondamentalement liée à la recherche des unités du corps quadratique Q (face=F0019 連d ). Après avoir établi que x 2 漣 dy 2 = m a une infinité de solutions entières pour au moins un m tel que |m | 麗 1 + 2 連d , on classe ces solutions modulo |m |, d’où l’existence des solutions de x 2 漣 dy 2 = 1.Si l’on associe aux solutions de x 2 漣 dy 2 = 1 les nombres 﨡 = x + y 連d , on voit qu’ils forment un groupe multiplicatif et on établit l’existence d’une solution fondamentale (x 1, y 1) telle que toutes les solutions de x 2 漣 dy 2 = 1 sont données par:
(appelée également équation de Pell-Fermat), où l’on suppose d sans facteur carré, joue un rôle particulier dans les équations du second degré; elle est, en effet, fondamentalement liée à la recherche des unités du corps quadratique Q (face=F0019 連d ). Après avoir établi que x 2 漣 dy 2 = m a une infinité de solutions entières pour au moins un m tel que |m | 麗 1 + 2 連d , on classe ces solutions modulo |m |, d’où l’existence des solutions de x 2 漣 dy 2 = 1.Si l’on associe aux solutions de x 2 漣 dy 2 = 1 les nombres 﨡 = x + y 連d , on voit qu’ils forment un groupe multiplicatif et on établit l’existence d’une solution fondamentale (x 1, y 1) telle que toutes les solutions de x 2 漣 dy 2 = 1 sont données par: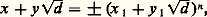 Pour m 1, l’équation peut ne pas avoir de solution (x 2 漣 3 y 2 = 漣 1 + 4 k par exemple, car x 2 漣 3 y 2 est congru à 0,1 ou 2, modulo 4). Si x 2 漣 dy 2 = 漣 1 est résolue en entiers, ses solutions seront données à partir d’une solution fondamentale (x 0, y 0) par:
Pour m 1, l’équation peut ne pas avoir de solution (x 2 漣 3 y 2 = 漣 1 + 4 k par exemple, car x 2 漣 3 y 2 est congru à 0,1 ou 2, modulo 4). Si x 2 漣 dy 2 = 漣 1 est résolue en entiers, ses solutions seront données à partir d’une solution fondamentale (x 0, y 0) par: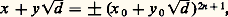 Le cas général x 2 漣 dy 2 = m , lorsqu’il aura des solutions, permettra de ranger celles-ci en un certain nombre s de classes, données par:
Le cas général x 2 漣 dy 2 = m , lorsqu’il aura des solutions, permettra de ranger celles-ci en un certain nombre s de classes, données par: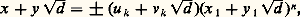 Le cas m = 梁 4 est plus directement lié aux unités de Q (face=F0019 連d ), qui se recherchent sous la forme (x + y 連d )/2, solution de 﨡2 + p 﨡 梁 1 = 0 avec p 2 梁 4 = u 2d . Il y a évidemment toujours des solutions pour m = + 4, données par:
Le cas m = 梁 4 est plus directement lié aux unités de Q (face=F0019 連d ), qui se recherchent sous la forme (x + y 連d )/2, solution de 﨡2 + p 﨡 梁 1 = 0 avec p 2 梁 4 = u 2d . Il y a évidemment toujours des solutions pour m = + 4, données par: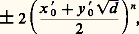 où n 捻 Z, avec (x 0, y 0) plus petite solution positive. Pour m = 漣 4, lorsqu’il y a solutions, elles s’exprimeront de même sous une forme:
où n 捻 Z, avec (x 0, y 0) plus petite solution positive. Pour m = 漣 4, lorsqu’il y a solutions, elles s’exprimeront de même sous une forme: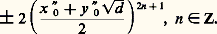 L’équation de Pell est aussi liée aux développements en fraction continuée de 連d . En effet, on établit que les solutions de x 2 漣 dy 2 = 1 correspondent à des réduites p n /q n du développement de 連d . Plus précisément, l’unité fondamentale de Q (face=F0019 連d ) est (x 0 = y 0 連d ), avec les notations précédentes, si le développement de 連d est de période impaire (il y a alors des solutions à x 2 漣 dy 2 = 漣 1), alors que c’est (x 1 + y 1 連d ), si la période est paire.Dans les deux cas, le développement de:
L’équation de Pell est aussi liée aux développements en fraction continuée de 連d . En effet, on établit que les solutions de x 2 漣 dy 2 = 1 correspondent à des réduites p n /q n du développement de 連d . Plus précisément, l’unité fondamentale de Q (face=F0019 連d ) est (x 0 = y 0 連d ), avec les notations précédentes, si le développement de 連d est de période impaire (il y a alors des solutions à x 2 漣 dy 2 = 漣 1), alors que c’est (x 1 + y 1 連d ), si la période est paire.Dans les deux cas, le développement de: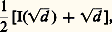 où I (face=F0019 連d ) est le plus grand nombre impair inférieur à 連d , fournit cette solution fondamentale par sa k -ième réduite, si la période est k .ConiquesL’équation:
où I (face=F0019 連d ) est le plus grand nombre impair inférieur à 連d , fournit cette solution fondamentale par sa k -ième réduite, si la période est k .ConiquesL’équation: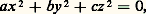 où l’on peut supposer a , b et c sans facteurs carrés et premiers entre eux deux à deux, conduit à un théorème de Legendre: une condition nécessaire et suffisante de résolubilité est que a , b , c ne soient pas de même signe et que 漣 bc , 漣 ca et 漣 ab soient respectivement résidus quadratiques de a , b et c (un résidu quadratique de 見 est un entier 廓 premier avec 見 tel que x 2 令 廓 mod 見 soit résoluble en x ; cf. DIVISIBILITÉ, chap. 4), et alors il y a une solution avec |x | 諒 連2|bc |, |y | 諒 連2ca , z 諒 連2|ab |. On a d’ailleurs là un cas particulier du théorème de Minkowski-Hasse, suivant lequel: une forme quadratique à coefficients rationnels représente zéro (c’est-à-dire s’annule pour un système de valeurs non toutes nulles des variables dans le corps considéré) dans le corps des rationnels si, et seulement si, elle représente zéro non trivialement dans tous les corps p -adiques et dans le corps des réels. C’est dire encore qu’une forme quadratique à coefficients entiers ne s’annulera pour des valeurs entières des variables que si, et seulement si, son égalité à zéro, modulo p m , est résoluble, quels que soient le nombre premier p et l’entier naturel m , en solutions entières non toutes divisibles par p . On dit alors que les conditions de congruence sont satisfaites.Ici encore on sait majorer la taille d’une plus petite solution. Un théorème de Chevalley, sur les formes de degré strictement inférieur au nombre des variables, permet d’affirmer que:
où l’on peut supposer a , b et c sans facteurs carrés et premiers entre eux deux à deux, conduit à un théorème de Legendre: une condition nécessaire et suffisante de résolubilité est que a , b , c ne soient pas de même signe et que 漣 bc , 漣 ca et 漣 ab soient respectivement résidus quadratiques de a , b et c (un résidu quadratique de 見 est un entier 廓 premier avec 見 tel que x 2 令 廓 mod 見 soit résoluble en x ; cf. DIVISIBILITÉ, chap. 4), et alors il y a une solution avec |x | 諒 連2|bc |, |y | 諒 連2ca , z 諒 連2|ab |. On a d’ailleurs là un cas particulier du théorème de Minkowski-Hasse, suivant lequel: une forme quadratique à coefficients rationnels représente zéro (c’est-à-dire s’annule pour un système de valeurs non toutes nulles des variables dans le corps considéré) dans le corps des rationnels si, et seulement si, elle représente zéro non trivialement dans tous les corps p -adiques et dans le corps des réels. C’est dire encore qu’une forme quadratique à coefficients entiers ne s’annulera pour des valeurs entières des variables que si, et seulement si, son égalité à zéro, modulo p m , est résoluble, quels que soient le nombre premier p et l’entier naturel m , en solutions entières non toutes divisibles par p . On dit alors que les conditions de congruence sont satisfaites.Ici encore on sait majorer la taille d’une plus petite solution. Un théorème de Chevalley, sur les formes de degré strictement inférieur au nombre des variables, permet d’affirmer que: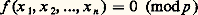 a une solution non nulle, si n 閭 3, pour toute forme quadratique. En combinant cela avec le lemme de Hensel (cf. théorie des NOMBRES-Nombres p -adiques), on voit que les conditions de congruence à vérifier sont en nombre fini.Dans le cas de deux variables:
a une solution non nulle, si n 閭 3, pour toute forme quadratique. En combinant cela avec le lemme de Hensel (cf. théorie des NOMBRES-Nombres p -adiques), on voit que les conditions de congruence à vérifier sont en nombre fini.Dans le cas de deux variables: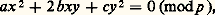 avec p 2, a une solution et une seule si, et seulement si, (ac 漣 b 2) est ou bien un multiple de p , ou bien l’opposé d’un résidu quadratique de p .Notons enfin que Dickson a établi que, si:
avec p 2, a une solution et une seule si, et seulement si, (ac 漣 b 2) est ou bien un multiple de p , ou bien l’opposé d’un résidu quadratique de p .Notons enfin que Dickson a établi que, si: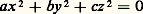 est résoluble, avec a , b , c premiers entre eux deux à deux et sans facteurs carrés, il s’ensuit que tout entier peut s’exprimer sous la forme ax 2 + by 2 + cz 2.Équation de PythagoreL’équation de Pythagore:
est résoluble, avec a , b , c premiers entre eux deux à deux et sans facteurs carrés, il s’ensuit que tout entier peut s’exprimer sous la forme ax 2 + by 2 + cz 2.Équation de PythagoreL’équation de Pythagore: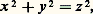 est un cas suffisamment classique pour qu’on s’y arrête. Si l’on suppose (x , y , z ) solution en entiers premiers entre eux, l’un des deux nombres x ou y est pair. Supposons que ce soit x . Il vient:
est un cas suffisamment classique pour qu’on s’y arrête. Si l’on suppose (x , y , z ) solution en entiers premiers entre eux, l’un des deux nombres x ou y est pair. Supposons que ce soit x . Il vient: qui entraîne:
qui entraîne: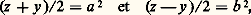 d’où les solutions générales positives données par:
d’où les solutions générales positives données par: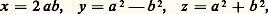 avec (a , b ) = 1, a 礪 b 礪 0 et a et b de parité différente. On trouve pour a = 2 et b = 1 la plus petite solution non banale: (4, 3, 5).Il est intéressant de signaler que l’étude du groupe orthogonal de la forme quadratique (x 2 + y 2 漣 z 2) conduit à envisager ici les matrices de ce groupe, à éléments entiers. On peut établir que, si:
avec (a , b ) = 1, a 礪 b 礪 0 et a et b de parité différente. On trouve pour a = 2 et b = 1 la plus petite solution non banale: (4, 3, 5).Il est intéressant de signaler que l’étude du groupe orthogonal de la forme quadratique (x 2 + y 2 漣 z 2) conduit à envisager ici les matrices de ce groupe, à éléments entiers. On peut établir que, si: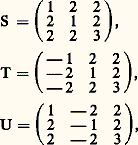 toutes les solutions entières, premières entre elles, de l’équation de Pythagore, peuvent s’obtenir à partir de la solution (3, 4, 5) par application répétée de S, T, U dans un ordre quelconque (cf. figure).Avant d’abandonner le second degré, citons l’équation:
toutes les solutions entières, premières entre elles, de l’équation de Pythagore, peuvent s’obtenir à partir de la solution (3, 4, 5) par application répétée de S, T, U dans un ordre quelconque (cf. figure).Avant d’abandonner le second degré, citons l’équation: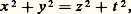 et, plus généralement, le système:
et, plus généralement, le système: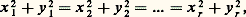 en liaison avec l’étude du nombre des représentations 福2(n ) d’un nombre n comme somme de deux carrés; on démontre que:
en liaison avec l’étude du nombre des représentations 福2(n ) d’un nombre n comme somme de deux carrés; on démontre que: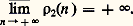 2. Le grand théorème de FermatPierre de Fermat (1601-1665) fut un mathématicien d’une érudition extraordinaire (géométrie analytique, fondements du calcul infinitésimal, lois de l’optique, fondements du calcul des probabilités et surtout théorie des nombres). Malheureusement, presque tous ses théorèmes étaient donnés sans démonstration, car il était alors d’usage de proposer ses découvertes à la sagacité de ses interlocuteurs (avec en particulier une rivalité très vive entre géomètres anglais et géomètres français). Le théorème élémentaire de Fermat (a p 漣 a est toujours divisible par p si p est premier), de même que toutes ses études sur les formes quadratiques et sur l’équation de Pell (appelée souvent Pell-Fermat) ont été vérifiés et établis par la suite, ainsi que toutes les propositions qu’il a affirmées, à l’exception de ce que l’on appelle le grand théorème de Fermat (on dit aussi le «dernier théorème de Fermat»).
2. Le grand théorème de FermatPierre de Fermat (1601-1665) fut un mathématicien d’une érudition extraordinaire (géométrie analytique, fondements du calcul infinitésimal, lois de l’optique, fondements du calcul des probabilités et surtout théorie des nombres). Malheureusement, presque tous ses théorèmes étaient donnés sans démonstration, car il était alors d’usage de proposer ses découvertes à la sagacité de ses interlocuteurs (avec en particulier une rivalité très vive entre géomètres anglais et géomètres français). Le théorème élémentaire de Fermat (a p 漣 a est toujours divisible par p si p est premier), de même que toutes ses études sur les formes quadratiques et sur l’équation de Pell (appelée souvent Pell-Fermat) ont été vérifiés et établis par la suite, ainsi que toutes les propositions qu’il a affirmées, à l’exception de ce que l’on appelle le grand théorème de Fermat (on dit aussi le «dernier théorème de Fermat»).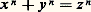 est impossible en nombres entiers avec xyz 0. L’auteur affirme cette proposition, en 1637, dans une annotation marginale des œuvres de Diophante; il y écrit: «J’ai découvert une démonstration assez remarquable de cette proposition, mais elle ne tiendrait pas dans cette marge.»Il suffirait d’établir ce théorème pour n = 4 et pour tout nombre premier p . Malheureusement, si la démonstration pour x 4 + y 4 = z 4 est assez simple par la méthode de descente infinie, si Euler et Gauss traitent le cas de p = 3 de même, si Legendre en 1823 met au point le cas de p = 5 (par montée infinie), le théorème n’est pas encore établi dans sa généralité, et l’on n’a pas pu non plus l’infirmer.Pour n = 4, la démonstration de Frénicle (1676) repose sur la descente infinie dont le principe était donné par Fermat: raisonnant sur l’équation de Pythagore (x 2)2 + (y 2)2 = z 2, on obtient, à partir de toute solution éventuelle (x 0, y 0, z 0), une nouvelle solution où |z 1| 麗 |z 0|, ce qui permet de conclure à l’impossibilité.Notons aussi l’impossibilité de x 4 + y 4 = 2 z 2, si x 2 y 2 (d’où l’impossibilité de trouver trois entiers dont les puissances quatrièmes soient en progression arithmétique de raison non nulle).De même x 4 + y 4 = 3 z 2 est impossible (comme x 2 + y 2 = 3 z 2) et, d’une manière plus générale, x 4 + y 4 = kz 2 est impossible pour 3 諒 k 諒 16, sauf k = 8 (études générales de Maillet en 1900).Pour n = 3, la démonstration ébauchée par Euler en 1774 fut précisée par Gauss. Comme dans le cas général de n premier quelconque, la recherche se scinde en deux étapes: on montre d’abord l’impossibilité en nombres non divisibles par 3; pour cela, on déduit de x 3 + y 3 = z 3 la congruence:
est impossible en nombres entiers avec xyz 0. L’auteur affirme cette proposition, en 1637, dans une annotation marginale des œuvres de Diophante; il y écrit: «J’ai découvert une démonstration assez remarquable de cette proposition, mais elle ne tiendrait pas dans cette marge.»Il suffirait d’établir ce théorème pour n = 4 et pour tout nombre premier p . Malheureusement, si la démonstration pour x 4 + y 4 = z 4 est assez simple par la méthode de descente infinie, si Euler et Gauss traitent le cas de p = 3 de même, si Legendre en 1823 met au point le cas de p = 5 (par montée infinie), le théorème n’est pas encore établi dans sa généralité, et l’on n’a pas pu non plus l’infirmer.Pour n = 4, la démonstration de Frénicle (1676) repose sur la descente infinie dont le principe était donné par Fermat: raisonnant sur l’équation de Pythagore (x 2)2 + (y 2)2 = z 2, on obtient, à partir de toute solution éventuelle (x 0, y 0, z 0), une nouvelle solution où |z 1| 麗 |z 0|, ce qui permet de conclure à l’impossibilité.Notons aussi l’impossibilité de x 4 + y 4 = 2 z 2, si x 2 y 2 (d’où l’impossibilité de trouver trois entiers dont les puissances quatrièmes soient en progression arithmétique de raison non nulle).De même x 4 + y 4 = 3 z 2 est impossible (comme x 2 + y 2 = 3 z 2) et, d’une manière plus générale, x 4 + y 4 = kz 2 est impossible pour 3 諒 k 諒 16, sauf k = 8 (études générales de Maillet en 1900).Pour n = 3, la démonstration ébauchée par Euler en 1774 fut précisée par Gauss. Comme dans le cas général de n premier quelconque, la recherche se scinde en deux étapes: on montre d’abord l’impossibilité en nombres non divisibles par 3; pour cela, on déduit de x 3 + y 3 = z 3 la congruence: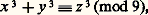 d’où:
d’où: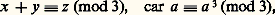 d’où:
d’où: La dernière étape est plus délicate et repose sur une descente infinie: on suppose une solution de x 3 + y 3 = z 3, avec |xyz | minimum et on pose:
La dernière étape est plus délicate et repose sur une descente infinie: on suppose une solution de x 3 + y 3 = z 3, avec |xyz | minimum et on pose:
 qui conduit à u 2 + 3 w 2 = s 3, si (u , 3) = 1. Si, au contraire, 3 divise u , on pose u = 3 v , d’où 18 v (3 v 2 + w 2) = z 3 conduisant à 3 v 2 + w 2 = s 3. Les solutions de s 3 = a 2 + 3 b 2, mises sous la forme:
qui conduit à u 2 + 3 w 2 = s 3, si (u , 3) = 1. Si, au contraire, 3 divise u , on pose u = 3 v , d’où 18 v (3 v 2 + w 2) = z 3 conduisant à 3 v 2 + w 2 = s 3. Les solutions de s 3 = a 2 + 3 b 2, mises sous la forme: conduisent alors à:
conduisent alors à: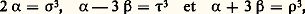 où 福3 + 精3 = 靖3, avec | 福靖精| 麗 |xyz |.Pour n = 5, la démonstration faite par Legendre en 1825 repose sur:
où 福3 + 精3 = 靖3, avec | 福靖精| 麗 |xyz |.Pour n = 5, la démonstration faite par Legendre en 1825 repose sur: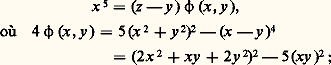 cela permet d’établir que 﨏 (x , y ) doit avoir des diviseurs aussi grands qu’on veut (méthode de montée infinie).La mathématicienne Sophie Germain a établi que, si n est premier ainsi que (2 n + 1), il faudrait, pour que l’équation de Fermat soit vérifiée, que x , y ou z soit divisible par n . Ce résultat a été généralisé par Legendre.Lamé, en 1837, établit le cas n = 7 après que Lejeune-Dirichlet ait démontré, en 1832, l’impossibilité pour n = 14.L’étude générale , pour n premier impair, comprend donc deux étapes. Dans la première étape, appelée souvent «premier cas du théorème», on démontre qu’il n’y a pas de solution parmi les entiers non multiples de n . Dans la deuxième étape, appelée «deuxième cas du théorème», on montre qu’il n’y a pas de solution dont l’un des nombres soit multiple de n . Cette étude générale fut entreprise par Kummer en 1844 et utilise le corps Q ( 福) des nombres algébriques de degré (n 漣 1) définis par l’équation 福n 漣 1 = 0. En effet, si 見 est une racine primitive n -ième de l’unité, l’équation de Fermat s’écrit:
cela permet d’établir que 﨏 (x , y ) doit avoir des diviseurs aussi grands qu’on veut (méthode de montée infinie).La mathématicienne Sophie Germain a établi que, si n est premier ainsi que (2 n + 1), il faudrait, pour que l’équation de Fermat soit vérifiée, que x , y ou z soit divisible par n . Ce résultat a été généralisé par Legendre.Lamé, en 1837, établit le cas n = 7 après que Lejeune-Dirichlet ait démontré, en 1832, l’impossibilité pour n = 14.L’étude générale , pour n premier impair, comprend donc deux étapes. Dans la première étape, appelée souvent «premier cas du théorème», on démontre qu’il n’y a pas de solution parmi les entiers non multiples de n . Dans la deuxième étape, appelée «deuxième cas du théorème», on montre qu’il n’y a pas de solution dont l’un des nombres soit multiple de n . Cette étude générale fut entreprise par Kummer en 1844 et utilise le corps Q ( 福) des nombres algébriques de degré (n 漣 1) définis par l’équation 福n 漣 1 = 0. En effet, si 見 est une racine primitive n -ième de l’unité, l’équation de Fermat s’écrit: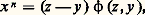 avec:
avec: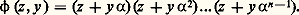 C’est en se plaçant dans Q ( 福) que Kummer essaya, à partir des entiers complexes m 0 + m 1 見 + ... + m n-1 見n-1 (m i entiers), de raisonner par décomposition en facteurs premiers de 﨏 (z , y ). Malheureusement, cette décomposition n’est pas toujours unique, et c’est à cette occasion que Kummer introduit la notion de nombre idéal [cf. ANNEAUX COMMUTATIFS]. Ces nombres idéaux, n’appartenant pas au corps envisagé, permettent la décomposition unique en facteurs idéaux premiers. Cette notion d’idéal fut précisée, un peu plus tard, d’un point de vue purement algébrique, par Dedekind.Kummer obtint des résultats spectaculaires, mais encore incomplets: le théorème de Fermat est vérifié pour tout premier p pour lesquels le nombre de classes d’idéaux n’est pas divisible par p (un tel nombre p est appelé nombre premier régulier). On ne sait pas, actuellement, s’il existe un nombre infini de nombres premiers réguliers; seuls 37, 59 et 67 sont non réguliers dans la première centaine. Mirimanoff en 1893 démontre le cas p = 37 en perfectionnant la méthode de Kummer. Actuellement, on a établi le théorème de Fermat pour tous les nombres premiers jusqu’à 125 000, et pour un certain nombre d’autres. On sait cependant (Terjanian) que l’équation x 2p + y 2p = z 2p , avec p premier, n’admet pas de solution ne divisant pas le produit xyz .3. Méthodes géométriquesPour classer les types d’équations, on utilise d’abord la dimension, ou nombre de variables indépendantes, du système proposé. Ainsi, en général, un système:
C’est en se plaçant dans Q ( 福) que Kummer essaya, à partir des entiers complexes m 0 + m 1 見 + ... + m n-1 見n-1 (m i entiers), de raisonner par décomposition en facteurs premiers de 﨏 (z , y ). Malheureusement, cette décomposition n’est pas toujours unique, et c’est à cette occasion que Kummer introduit la notion de nombre idéal [cf. ANNEAUX COMMUTATIFS]. Ces nombres idéaux, n’appartenant pas au corps envisagé, permettent la décomposition unique en facteurs idéaux premiers. Cette notion d’idéal fut précisée, un peu plus tard, d’un point de vue purement algébrique, par Dedekind.Kummer obtint des résultats spectaculaires, mais encore incomplets: le théorème de Fermat est vérifié pour tout premier p pour lesquels le nombre de classes d’idéaux n’est pas divisible par p (un tel nombre p est appelé nombre premier régulier). On ne sait pas, actuellement, s’il existe un nombre infini de nombres premiers réguliers; seuls 37, 59 et 67 sont non réguliers dans la première centaine. Mirimanoff en 1893 démontre le cas p = 37 en perfectionnant la méthode de Kummer. Actuellement, on a établi le théorème de Fermat pour tous les nombres premiers jusqu’à 125 000, et pour un certain nombre d’autres. On sait cependant (Terjanian) que l’équation x 2p + y 2p = z 2p , avec p premier, n’admet pas de solution ne divisant pas le produit xyz .3. Méthodes géométriquesPour classer les types d’équations, on utilise d’abord la dimension, ou nombre de variables indépendantes, du système proposé. Ainsi, en général, un système: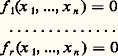 est de dimension (n 漣 r ). En dimension 1, on parle de courbes ; en dimension 2, de surfaces [cf. GÉOMÉTRIE ALGÉBRIQUE]. Les solutions en nombres entiers ou rationnels du système proposé ne sont autres que les points entiers ou rationnels de la variété algébrique associée.Déjà pour les courbes planes (une équation f (x , y ) = 0), la classification par le degré s’avère trop grossière. Ainsi la théorie des cubiques planes à point double, comme:
est de dimension (n 漣 r ). En dimension 1, on parle de courbes ; en dimension 2, de surfaces [cf. GÉOMÉTRIE ALGÉBRIQUE]. Les solutions en nombres entiers ou rationnels du système proposé ne sont autres que les points entiers ou rationnels de la variété algébrique associée.Déjà pour les courbes planes (une équation f (x , y ) = 0), la classification par le degré s’avère trop grossière. Ainsi la théorie des cubiques planes à point double, comme: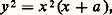 avec a rationnel, est très simple, celle des cubiques planes sans point double, comme:
avec a rationnel, est très simple, celle des cubiques planes sans point double, comme: avec a et b rationnels non nuls et distincts, est beaucoup plus délicate [cf. COURBES ALGÉBRIQUES]. On est ainsi amené à utiliser des «invariants» de nature géométrique. Pour les courbes, on utilise le genre, nombre de trous de la surface de Riemann correspondante. Pour une courbe plane de degré d , à points multiples ordinaires, le genre vaut:
avec a et b rationnels non nuls et distincts, est beaucoup plus délicate [cf. COURBES ALGÉBRIQUES]. On est ainsi amené à utiliser des «invariants» de nature géométrique. Pour les courbes, on utilise le genre, nombre de trous de la surface de Riemann correspondante. Pour une courbe plane de degré d , à points multiples ordinaires, le genre vaut: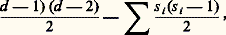 où la sommation s’étend à tous les points multiples, l’ordre de ceux-ci étant s i .Courbes de genre zéroOn dispose ici d’une analyse complète. En ce qui concerne les points rationnels, la démarche est la suivante. Toute courbe de genre zéro peut, par un changement de variables, être ramenée à une conique plane (D. Hilbert-A. Hurwitz, 1891), soit ax 2 + by 2 + c = 0. D’après le théorème de Legendre (cf. supra ), les conditions de congruence permettent de décider si cette conique a un point rationnel. S’il y a un point rationnel, soit M0, on peut les décrire tous, au moyen d’une paramétrisation biunivoque:
où la sommation s’étend à tous les points multiples, l’ordre de ceux-ci étant s i .Courbes de genre zéroOn dispose ici d’une analyse complète. En ce qui concerne les points rationnels, la démarche est la suivante. Toute courbe de genre zéro peut, par un changement de variables, être ramenée à une conique plane (D. Hilbert-A. Hurwitz, 1891), soit ax 2 + by 2 + c = 0. D’après le théorème de Legendre (cf. supra ), les conditions de congruence permettent de décider si cette conique a un point rationnel. S’il y a un point rationnel, soit M0, on peut les décrire tous, au moyen d’une paramétrisation biunivoque: avec f et g des quotients de polynômes à coefficients rationnels (chaque point rationnel de la conique correspond à une unique valeur, rationnelle, du paramètre t ). Une telle paramétrisation sera dite polynomiale. Pour obtenir cette paramétrisation, on fait simplement tourner une droite autour de M0; chaque droite de pente rationnelle t , passant par M0, recoupe la conique, qui est de degré 2, en un unique point, à coordonnées (x = f (t ), y = g (t )) rationnelles. C’est ainsi qu’a été résolue plus haut l’équation de Pythagore.Pour les points entiers sur une courbe de genre zéro, on dispose aussi d’une analyse complète (C. L. Siegel, 1929): essentiellement, l’équation de Pell (cf. supra ) est le seul cas non évident où il peut y avoir une infinité de points entiers.Courbes de genre 1: points rationnelsIci, les conditions de congruence ne suffisent plus à assurer l’existence d’un point rationnel, comme le montre l’exemple 3 x 3 + 4 y 3 + 5 = 0 (E. S. Selmer, 1951). On dispose cependant d’un procédé remontant à Fermat (descente infinie) permettant d’étudier de telles courbes. C’est un problème ouvert de savoir si l’application systématique de ce procédé, conjointement avec les conditions de congruence, suffit toujours à déterminer la présence ou l’absence d’un point rationnel sur une courbe de genre 1.Si l’on connaît un point rationnel sur une telle courbe, celle-ci peut être ramenée (Poincaré, 1901) à une cubique plane non singulière:
avec f et g des quotients de polynômes à coefficients rationnels (chaque point rationnel de la conique correspond à une unique valeur, rationnelle, du paramètre t ). Une telle paramétrisation sera dite polynomiale. Pour obtenir cette paramétrisation, on fait simplement tourner une droite autour de M0; chaque droite de pente rationnelle t , passant par M0, recoupe la conique, qui est de degré 2, en un unique point, à coordonnées (x = f (t ), y = g (t )) rationnelles. C’est ainsi qu’a été résolue plus haut l’équation de Pythagore.Pour les points entiers sur une courbe de genre zéro, on dispose aussi d’une analyse complète (C. L. Siegel, 1929): essentiellement, l’équation de Pell (cf. supra ) est le seul cas non évident où il peut y avoir une infinité de points entiers.Courbes de genre 1: points rationnelsIci, les conditions de congruence ne suffisent plus à assurer l’existence d’un point rationnel, comme le montre l’exemple 3 x 3 + 4 y 3 + 5 = 0 (E. S. Selmer, 1951). On dispose cependant d’un procédé remontant à Fermat (descente infinie) permettant d’étudier de telles courbes. C’est un problème ouvert de savoir si l’application systématique de ce procédé, conjointement avec les conditions de congruence, suffit toujours à déterminer la présence ou l’absence d’un point rationnel sur une courbe de genre 1.Si l’on connaît un point rationnel sur une telle courbe, celle-ci peut être ramenée (Poincaré, 1901) à une cubique plane non singulière: avec P(x ) un polynôme du troisième degré sans facteur multiple. On a là une courbe elliptique, objet fondamental tant en géométrie algébrique qu’en théorie des nombres. La géométrie algébrique montre qu’on ne peut pas ramener une telle courbe à une courbe de genre zéro. Il existe pourtant une paramétrisation des solutions complexes de (C), bien classique, mais, elle, de nature transcendante: la paramétrisation par les fonctions elliptiques (Weierstrass), [cf. COURBES ALGÉBRIQUES]. On voit sur cette paramétrisation que les solutions complexes de (C) peuvent être munies d’une structure de groupe abélien. En fait, la composition ainsi définie induit une composition des points rationnels de la cubique. Essentiellement, il s’agit de la construction suivante. Étant donné deux points rationnels de la cubique, la droite qui les joint, qui est à coefficients rationnels, recoupe la cubique en un troisième point, dont les coordonnées sont par force rationnelles: c’est le procédé de la corde pour engendrer de nouvelles solutions (on peut aussi utiliser la tangente en un point rationnel). On obtient ainsi une structure de groupe abélien sur l’ensemble des points rationnels de (C). L’important théorème de Mordell (1922), généralisé par Weil (1928), établi par descente infinie, dit que ce groupe appelé depuis groupe de Mordell-Weil, admet un nombre fini de générateurs. En d’autres termes, étant donné une cubique (C), il existe un nombre fini de points rationnels situés dessus tels que tous les autres points rationnels de (C) puissent être obtenus à partir de ceux-ci par itération du procédé de la corde et de la tangente. Étant donné une courbe (C), on sait borner le nombre minimal de générateurs du groupe de Mordell-Weil associé (rang ), mais on n’a pas de méthode générale pour déterminer le rang, a fortiori pour construire explicitement un système de générateurs. On dispose seulement d’un algorithme conditionnel (Yu. I. Manin, 1973), reposant sur deux conjectures. L’une, de Weil, relie les courbes elliptiques aux formes modulaires. L’autre, de B. Birch et H. P. F. Swinnerton-Dyer (1965), affirme que le rang d’une courbe elliptique est donné par l’ordre du zéro au point complexe z = 1 d’une certaine fonction méromorphe dont la définition fait intervenir le nombre de solutions modulo p , nombre premier, de l’équation (C), cela pour tous les nombres premiers p (cf. fonction ZETA). L’ordinateur a donné un grand poids à cette conjecture, et des progrès théoriques ont été effectués.Courbes de genre au moins égal à 2: points rationnelsParmi les courbes de genre au moins égal à 2, on trouve les courbes planes non singulières de degré au moins 4. Là encore, on ne peut ramener l’étude de telles courbes à l’étude de celles de genre inférieur ou égal à 1. On ne dispose d’aucun procédé permettant d’engendrer un nombre infini de solutions à partir d’un nombre fini d’entre elles. Mordell a ainsi conjecturé (1922) qu’une telle équation n’admettrait jamais qu’un nombre fini de solutions rationnelles. Cette conjecture a été démontrée par G. Faldings en juin 1983.Points entiers sur les courbes de genre au moins 1On dispose du théorème général de C. L. Siegel (1929) selon lequel une telle courbe n’a qu’un nombre fini de points entiers. La démonstration utilise d’une part le théorème de A. Weil (1928), étendant celui de Mordell, d’autre part la mauvaise approximation par des rationnels des irrationnels algébriques (cf. approximations DIOPHANTIENNES). Ce résultat englobe celui de Thue (1909), lui aussi fondé sur les approximations diophantiennes: l’équation
avec P(x ) un polynôme du troisième degré sans facteur multiple. On a là une courbe elliptique, objet fondamental tant en géométrie algébrique qu’en théorie des nombres. La géométrie algébrique montre qu’on ne peut pas ramener une telle courbe à une courbe de genre zéro. Il existe pourtant une paramétrisation des solutions complexes de (C), bien classique, mais, elle, de nature transcendante: la paramétrisation par les fonctions elliptiques (Weierstrass), [cf. COURBES ALGÉBRIQUES]. On voit sur cette paramétrisation que les solutions complexes de (C) peuvent être munies d’une structure de groupe abélien. En fait, la composition ainsi définie induit une composition des points rationnels de la cubique. Essentiellement, il s’agit de la construction suivante. Étant donné deux points rationnels de la cubique, la droite qui les joint, qui est à coefficients rationnels, recoupe la cubique en un troisième point, dont les coordonnées sont par force rationnelles: c’est le procédé de la corde pour engendrer de nouvelles solutions (on peut aussi utiliser la tangente en un point rationnel). On obtient ainsi une structure de groupe abélien sur l’ensemble des points rationnels de (C). L’important théorème de Mordell (1922), généralisé par Weil (1928), établi par descente infinie, dit que ce groupe appelé depuis groupe de Mordell-Weil, admet un nombre fini de générateurs. En d’autres termes, étant donné une cubique (C), il existe un nombre fini de points rationnels situés dessus tels que tous les autres points rationnels de (C) puissent être obtenus à partir de ceux-ci par itération du procédé de la corde et de la tangente. Étant donné une courbe (C), on sait borner le nombre minimal de générateurs du groupe de Mordell-Weil associé (rang ), mais on n’a pas de méthode générale pour déterminer le rang, a fortiori pour construire explicitement un système de générateurs. On dispose seulement d’un algorithme conditionnel (Yu. I. Manin, 1973), reposant sur deux conjectures. L’une, de Weil, relie les courbes elliptiques aux formes modulaires. L’autre, de B. Birch et H. P. F. Swinnerton-Dyer (1965), affirme que le rang d’une courbe elliptique est donné par l’ordre du zéro au point complexe z = 1 d’une certaine fonction méromorphe dont la définition fait intervenir le nombre de solutions modulo p , nombre premier, de l’équation (C), cela pour tous les nombres premiers p (cf. fonction ZETA). L’ordinateur a donné un grand poids à cette conjecture, et des progrès théoriques ont été effectués.Courbes de genre au moins égal à 2: points rationnelsParmi les courbes de genre au moins égal à 2, on trouve les courbes planes non singulières de degré au moins 4. Là encore, on ne peut ramener l’étude de telles courbes à l’étude de celles de genre inférieur ou égal à 1. On ne dispose d’aucun procédé permettant d’engendrer un nombre infini de solutions à partir d’un nombre fini d’entre elles. Mordell a ainsi conjecturé (1922) qu’une telle équation n’admettrait jamais qu’un nombre fini de solutions rationnelles. Cette conjecture a été démontrée par G. Faldings en juin 1983.Points entiers sur les courbes de genre au moins 1On dispose du théorème général de C. L. Siegel (1929) selon lequel une telle courbe n’a qu’un nombre fini de points entiers. La démonstration utilise d’une part le théorème de A. Weil (1928), étendant celui de Mordell, d’autre part la mauvaise approximation par des rationnels des irrationnels algébriques (cf. approximations DIOPHANTIENNES). Ce résultat englobe celui de Thue (1909), lui aussi fondé sur les approximations diophantiennes: l’équation où f est un polynôme homogène irréductible à coefficients entiers de degré au moins égal à 3, et m est un entier non nul, ne possède qu’un nombre fini de solutions entières.Dans beaucoup de cas, en particulier pour les équations y 2 = P(x ) où le polynôme P a au moins trois zéros distincts, A. Baker a donné des majorations effectives (mais grandes) pour la taille possible des solutions entières; ainsi, pour l’équation de Thue ci-dessus:
où f est un polynôme homogène irréductible à coefficients entiers de degré au moins égal à 3, et m est un entier non nul, ne possède qu’un nombre fini de solutions entières.Dans beaucoup de cas, en particulier pour les équations y 2 = P(x ) où le polynôme P a au moins trois zéros distincts, A. Baker a donné des majorations effectives (mais grandes) pour la taille possible des solutions entières; ainsi, pour l’équation de Thue ci-dessus: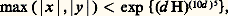 où d est le degré de f , et H un entier dépendant de la taille de m et des coefficients de f . Dans certains cas particuliers, ces méthodes permettent même de trouver toutes les solutions entières.Surfaces rationnellesLes surfaces rationnelles sont les analogues en dimension 2 des courbes unicursales, celles qui peuvent être paramétrées de façon polynomiale si l’on autorise les coefficients des polynômes définissant le paramétrage à être des nombres complexes. Parmi celle-ci, on trouve les surfaces non singulières de l’espace ordinaire définies par une équation de degré 2 (quadriques) ou 3 (surfaces cubiques), mais aussi des équations de degré supérieur, comme:
où d est le degré de f , et H un entier dépendant de la taille de m et des coefficients de f . Dans certains cas particuliers, ces méthodes permettent même de trouver toutes les solutions entières.Surfaces rationnellesLes surfaces rationnelles sont les analogues en dimension 2 des courbes unicursales, celles qui peuvent être paramétrées de façon polynomiale si l’on autorise les coefficients des polynômes définissant le paramétrage à être des nombres complexes. Parmi celle-ci, on trouve les surfaces non singulières de l’espace ordinaire définies par une équation de degré 2 (quadriques) ou 3 (surfaces cubiques), mais aussi des équations de degré supérieur, comme: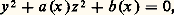 On est loin de disposer ici de résultats aussi satisfaisants que pour les courbes de genre zéro. Dans certains cas: quadriques (Hasse-Minkowski, cf. supra ), surfaces cubiques
On est loin de disposer ici de résultats aussi satisfaisants que pour les courbes de genre zéro. Dans certains cas: quadriques (Hasse-Minkowski, cf. supra ), surfaces cubiques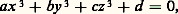 avec ab = cd 0 (E. S. Selmer, 1953), les conditions de congruence (et la condition réelle) suffisent à assurer l’existence de points rationnels. Cela ne vaut pas en général, comme le montre l’exemple (J. W. S. Cassels-M. J.T. Guy, 1966):
avec ab = cd 0 (E. S. Selmer, 1953), les conditions de congruence (et la condition réelle) suffisent à assurer l’existence de points rationnels. Cela ne vaut pas en général, comme le montre l’exemple (J. W. S. Cassels-M. J.T. Guy, 1966): Si une quadrique a un point rationnel, on peut encore donner une paramétrisation polynomiale essentiellement biunivoque des points rationnels, en utilisant la même méthode que pour les coniques.Une telle paramétrisation est encore possible pour une surface cubique de l’espace ordinaire, soit , qui contient deux droites D et D définies par des équations à coefficients rationnels, et ne se coupant pas. Choisissons un plan 神, d’équation ax + by + cz + d = 0, avec a , b , c , d rationnels. Pour M un point rationnel du plan 神, la droite DM, intersection des deux plans engendrés l’un par (M, D), l’autre par (M, D ), est définie par des équations à coefficients rationnels. Elle coupe la surface cubique en trois points: celui qui est situé sur D et celui qui est situé sur D’ sont définis par des équations à coefficients rationnels, le troisième, soit f (M), est donc à coordonnées rationnelles. On vérifie que la correspondance qui à M associe f (M) définit une paramétrisation polynomiale essentiellement biunivoque des points rationnels de par ceux de 神. C’est ainsi qu’on trouve la solution générale due à Euler de l’équation: x 3 + y 3 + z 3 = 1
Si une quadrique a un point rationnel, on peut encore donner une paramétrisation polynomiale essentiellement biunivoque des points rationnels, en utilisant la même méthode que pour les coniques.Une telle paramétrisation est encore possible pour une surface cubique de l’espace ordinaire, soit , qui contient deux droites D et D définies par des équations à coefficients rationnels, et ne se coupant pas. Choisissons un plan 神, d’équation ax + by + cz + d = 0, avec a , b , c , d rationnels. Pour M un point rationnel du plan 神, la droite DM, intersection des deux plans engendrés l’un par (M, D), l’autre par (M, D ), est définie par des équations à coefficients rationnels. Elle coupe la surface cubique en trois points: celui qui est situé sur D et celui qui est situé sur D’ sont définis par des équations à coefficients rationnels, le troisième, soit f (M), est donc à coordonnées rationnelles. On vérifie que la correspondance qui à M associe f (M) définit une paramétrisation polynomiale essentiellement biunivoque des points rationnels de par ceux de 神. C’est ainsi qu’on trouve la solution générale due à Euler de l’équation: x 3 + y 3 + z 3 = 1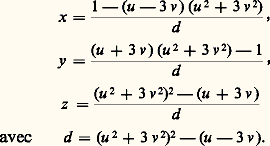 Des méthodes fines de géométrie algébrique montrent qu’une telle paramétrisation polynomiale biunivoque à coefficients rationnels est souvent impossible, ainsi pour:
Des méthodes fines de géométrie algébrique montrent qu’une telle paramétrisation polynomiale biunivoque à coefficients rationnels est souvent impossible, ainsi pour: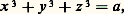 où a est un rationnel qui n’est pas un cube (Yu. I. Manin, 1970). On peut cependant, pour une surface cubique non singulière qui possède au moins un point rationnel, trouver des familles polynomiales à deux vrais paramètres (c’est-à-dire qu’on ne peut réduire à un seul paramètre), soit:
où a est un rationnel qui n’est pas un cube (Yu. I. Manin, 1970). On peut cependant, pour une surface cubique non singulière qui possède au moins un point rationnel, trouver des familles polynomiales à deux vrais paramètres (c’est-à-dire qu’on ne peut réduire à un seul paramètre), soit: avec A,B,C quotients de polynômes en u et y à coefficients rationnels, mais en général même un nombre fini de telles familles ne suffit pas à décrire tous les points rationnels de la surface cubique. On obtient néanmoins beaucoup de solutions rationnelles. En spécialisant les paramètres, on obtient par exemple que tout rationnel est somme de trois cubes de rationnels:
avec A,B,C quotients de polynômes en u et y à coefficients rationnels, mais en général même un nombre fini de telles familles ne suffit pas à décrire tous les points rationnels de la surface cubique. On obtient néanmoins beaucoup de solutions rationnelles. En spécialisant les paramètres, on obtient par exemple que tout rationnel est somme de trois cubes de rationnels: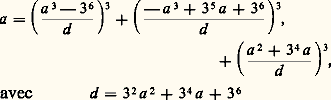 (Ryley, 1825; H. W. Richmond, 1930).En s’inspirant de la méthode de Mordell-Weil, F. Châtelet (1959) a montré qu’un nombre fini de solutions paramétriques polynomiales (à 4 variables) permet de décrire toutes les solutions rationnelles de:
(Ryley, 1825; H. W. Richmond, 1930).En s’inspirant de la méthode de Mordell-Weil, F. Châtelet (1959) a montré qu’un nombre fini de solutions paramétriques polynomiales (à 4 variables) permet de décrire toutes les solutions rationnelles de: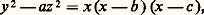 avec a , b , c rationnels non nuls. On ignore par contre si une solution polynomiale, même partielle, à deux vrais paramètres et à coefficients rationnels est possible pour l’équation générale:
avec a , b , c rationnels non nuls. On ignore par contre si une solution polynomiale, même partielle, à deux vrais paramètres et à coefficients rationnels est possible pour l’équation générale: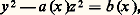 Pour les points entiers des surfaces cubiques, on a des résultats épars. Soit par exemple l’équation:
Pour les points entiers des surfaces cubiques, on a des résultats épars. Soit par exemple l’équation: avec n entier fixé, à résoudre en (x , y , z ) entiers. On voit facilement (congruences modulo 9) qu’il n’y a pas de solutions si n est congru à 梁 4 modulo 9. Sinon, on ne sait pas s’il y a toujours une solution, par exemple pour n = 30, et, s’il y en a une, s’il y en a une infinité. L’identité:
avec n entier fixé, à résoudre en (x , y , z ) entiers. On voit facilement (congruences modulo 9) qu’il n’y a pas de solutions si n est congru à 梁 4 modulo 9. Sinon, on ne sait pas s’il y a toujours une solution, par exemple pour n = 30, et, s’il y en a une, s’il y en a une infinité. L’identité: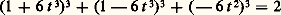 donne une infinité de solutions pour n = 2, mais, pour n = 3, on ne connaît que les solutions (1, 1, 1) et (4, 4, 漣 5).Pour:
donne une infinité de solutions pour n = 2, mais, pour n = 3, on ne connaît que les solutions (1, 1, 1) et (4, 4, 漣 5).Pour: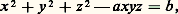 avec a et b entiers, on dispose d’un processus (Markov, Hurwitz) permettant d’engendrer toutes les solutions entières à partir d’un nombre fini, explicitement calculables, d’entre elles.On conjecture (P. Erdös, E. G. Straus) que l’équation:
avec a et b entiers, on dispose d’un processus (Markov, Hurwitz) permettant d’engendrer toutes les solutions entières à partir d’un nombre fini, explicitement calculables, d’entre elles.On conjecture (P. Erdös, E. G. Straus) que l’équation: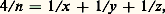 avec n entier fixé, n 礪 1, à résoudre en entiers positifs x , y , z , a toujours des solutions (c’est un cas particulier du problème des fractions égyptiennes , où l’on cherche à écrire un rationnel comme somme d’un nombre donné d’inverses d’entiers). Cette conjecture a été établie pour n 諒 108.Surfaces analogues aux courbes de genre 1L’analogue immédiat, du point de vue de la géométrie algébrique, consiste en les surfaces abéliennes (pour lesquelles il est difficile de donner des équations!). Le théorème de A. Weil (1928) nous renseigne sur les points rationnels, mais on ignore s’il n’y a qu’un nombre fini de points entiers.Un autre analogue consiste en les surfaces non singulières de l’espace ordinaire, de degré 4. Une conjecture d’Euler affirme que l’équation:
avec n entier fixé, n 礪 1, à résoudre en entiers positifs x , y , z , a toujours des solutions (c’est un cas particulier du problème des fractions égyptiennes , où l’on cherche à écrire un rationnel comme somme d’un nombre donné d’inverses d’entiers). Cette conjecture a été établie pour n 諒 108.Surfaces analogues aux courbes de genre 1L’analogue immédiat, du point de vue de la géométrie algébrique, consiste en les surfaces abéliennes (pour lesquelles il est difficile de donner des équations!). Le théorème de A. Weil (1928) nous renseigne sur les points rationnels, mais on ignore s’il n’y a qu’un nombre fini de points entiers.Un autre analogue consiste en les surfaces non singulières de l’espace ordinaire, de degré 4. Une conjecture d’Euler affirme que l’équation: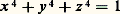 n’a pas d’autres solutions rationnelles que (face=F0019 梁 1, 0, 0), (0, 梁 1, 0) et (0, 0, 梁 1), mais on sait seulement qu’une autre solution devrait avoir un dénominateur au moins égal à 220 000. Euler donna une infinité de solutions rationnelles de:
n’a pas d’autres solutions rationnelles que (face=F0019 梁 1, 0, 0), (0, 梁 1, 0) et (0, 0, 梁 1), mais on sait seulement qu’une autre solution devrait avoir un dénominateur au moins égal à 220 000. Euler donna une infinité de solutions rationnelles de: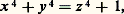 au moyen d’une solution à un paramètre; par exemple:
au moyen d’une solution à un paramètre; par exemple: La géométrie algébrique montre qu’aucune solution, même partielle, polynomiale à deux vrais paramètres n’est possible. Cependant, en utilisant le fait que la surface ci-dessus peut être fibrée en courbes elliptiques, on peut donner une infinité de solutions essentiellement distinctes à un paramètre (H. P. F. Swinnerton-Dyer, 1971).Surfaces analogues aux courbes de genre au moins 2Parmi celles-ci, on trouve les surfaces non singulières d’équation:
La géométrie algébrique montre qu’aucune solution, même partielle, polynomiale à deux vrais paramètres n’est possible. Cependant, en utilisant le fait que la surface ci-dessus peut être fibrée en courbes elliptiques, on peut donner une infinité de solutions essentiellement distinctes à un paramètre (H. P. F. Swinnerton-Dyer, 1971).Surfaces analogues aux courbes de genre au moins 2Parmi celles-ci, on trouve les surfaces non singulières d’équation: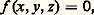 avec f de degré au moins 5. Une fois de plus, elles ne peuvent être ramenées aux surfaces précédentes. Il peut exister des solutions à un paramètre, mais une conjecture analogue à celle de Mordell pour les courbes de genre au moins 2 voudrait que, pour une telle surface, les points rationnels soient concentrés sur un nombre fini de courbes algébriques tracées sur la surface.4. Équations à beaucoup de variablesLa méthode du cercle de Hardy-Littlewood-Vinogradov, qui avait déjà révélé sa puissance dans l’étude du problème de Waring (cf. théorie des NOMBRES – Théorie analytique des nombres), a aussi permis d’obtenir le résultat suivant (H. Davenport, B. Birch, 1962). Soit f 1, ..., f r des formes homogènes de degré d , en n variables, à coefficients entiers. Supposons que le système:
avec f de degré au moins 5. Une fois de plus, elles ne peuvent être ramenées aux surfaces précédentes. Il peut exister des solutions à un paramètre, mais une conjecture analogue à celle de Mordell pour les courbes de genre au moins 2 voudrait que, pour une telle surface, les points rationnels soient concentrés sur un nombre fini de courbes algébriques tracées sur la surface.4. Équations à beaucoup de variablesLa méthode du cercle de Hardy-Littlewood-Vinogradov, qui avait déjà révélé sa puissance dans l’étude du problème de Waring (cf. théorie des NOMBRES – Théorie analytique des nombres), a aussi permis d’obtenir le résultat suivant (H. Davenport, B. Birch, 1962). Soit f 1, ..., f r des formes homogènes de degré d , en n variables, à coefficients entiers. Supposons que le système: n’a pas de solution complexe singulière non nulle. Si les conditions de congruence sont satisfaites, si le système a une solution non nulle en nombres réels et si:
n’a pas de solution complexe singulière non nulle. Si les conditions de congruence sont satisfaites, si le système a une solution non nulle en nombres réels et si: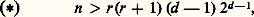 alors le système a une solution non nulle en nombres entiers. On peut appliquer ce résultat par exemple à une forme cubique en au moins 17 variables (toute forme telle a un zéro non trivial), ou à un système de deux formes quadratiques en au moins 13 variables.Si les conditions de congruence (et la condition réelle) ne sont pas en général suffisantes quand le nombre de variables est très petit par rapport au degré (ainsi r = 1, d = 3, n = 4, cf. supra ), on peut se demander si on ne peut pas affaiblir l’inégalité (). On ignore ainsi si, pour une forme cubique non singulière en au moins 5 variables, les conditions de congruence sont suffisantes.On se demande si une équation non singulière:
alors le système a une solution non nulle en nombres entiers. On peut appliquer ce résultat par exemple à une forme cubique en au moins 17 variables (toute forme telle a un zéro non trivial), ou à un système de deux formes quadratiques en au moins 13 variables.Si les conditions de congruence (et la condition réelle) ne sont pas en général suffisantes quand le nombre de variables est très petit par rapport au degré (ainsi r = 1, d = 3, n = 4, cf. supra ), on peut se demander si on ne peut pas affaiblir l’inégalité (). On ignore ainsi si, pour une forme cubique non singulière en au moins 5 variables, les conditions de congruence sont suffisantes.On se demande si une équation non singulière: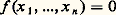 de degré d 諒 n a une infinité de solutions rationnelles dès qu’elle en a une. Considérons par exemple l’équation:
de degré d 諒 n a une infinité de solutions rationnelles dès qu’elle en a une. Considérons par exemple l’équation: Pour d = n = 4, à part les solutions évidentes du type (1, 0, ..., 0), on connaît:
Pour d = n = 4, à part les solutions évidentes du type (1, 0, ..., 0), on connaît: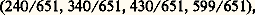 mais on ne connaît pas de solution à un paramètre. Pour d = n = 5, on connaît des solutions à deux paramètres. On connaît par ailleurs beaucoup de solutions de l’équation u 6 + v 6 + w 6 = z 6 + t 6 + 1 (A. Bremner, 1980), par une méthode inspirée de celle qui est mentionnée pour l’équation x 4 + y 4 = z 4 + 1.5. Équations diophantiennes exponentiellesOn appelle ainsi les équations du type:
mais on ne connaît pas de solution à un paramètre. Pour d = n = 5, on connaît des solutions à deux paramètres. On connaît par ailleurs beaucoup de solutions de l’équation u 6 + v 6 + w 6 = z 6 + t 6 + 1 (A. Bremner, 1980), par une méthode inspirée de celle qui est mentionnée pour l’équation x 4 + y 4 = z 4 + 1.5. Équations diophantiennes exponentiellesOn appelle ainsi les équations du type: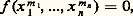 où f est un polynôme en n variables à coefficients entiers, à résoudre en entiers positifs (x 1, ..., x n , m 1, ..., m n ).Comme équations classiques de ce type, résolubles par des factorisations en nombres entiers, citons:
où f est un polynôme en n variables à coefficients entiers, à résoudre en entiers positifs (x 1, ..., x n , m 1, ..., m n ).Comme équations classiques de ce type, résolubles par des factorisations en nombres entiers, citons: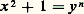
 Pour établir une conjecture de Ramanujan l’équation:
Pour établir une conjecture de Ramanujan l’équation: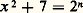 n’a pour solutions que n = 3, 4, 5, 7, 15, Nagell (1960) eut recours à la théorie algébrique des nombres (calculs dans le corps Q (face=F0019 連漣 7).Les résultats d’A. Baker sur les formes linéaires de logarithmes ont permis de réaliser d’importants progrès (cf. nombres TRANSCENDANTS). Il s’agit en fait de méthodes d’approximation.Ainsi, pour f (x ) un polynôme à coefficients entiers avec au moins deux zéros, on sait (A. Schinzel, R. Tijdeman, 1976) qu’il n’y a qu’un nombre fini d’entiers m pour lesquels l’équation:
n’a pour solutions que n = 3, 4, 5, 7, 15, Nagell (1960) eut recours à la théorie algébrique des nombres (calculs dans le corps Q (face=F0019 連漣 7).Les résultats d’A. Baker sur les formes linéaires de logarithmes ont permis de réaliser d’importants progrès (cf. nombres TRANSCENDANTS). Il s’agit en fait de méthodes d’approximation.Ainsi, pour f (x ) un polynôme à coefficients entiers avec au moins deux zéros, on sait (A. Schinzel, R. Tijdeman, 1976) qu’il n’y a qu’un nombre fini d’entiers m pour lesquels l’équation: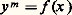 a des solutions avec y 礪 1.En 1976, R. Tijdeman, utilisant ces méthodes, a montré que l’équation de Catalan:
a des solutions avec y 礪 1.En 1976, R. Tijdeman, utilisant ces méthodes, a montré que l’équation de Catalan: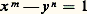
Encyclopédie Universelle. 2012.
